Understanding DEX Price Slippage

You are currently viewing Understanding DEX Price Slippage

Estimating Price Impact in Decentralized Exchanges

To properly evaluate price impact on a decentralized exchange (DEX), we’ll continue our analysis assuming zero trading fees. Consider a liquidity pool with:

Consider a liquidity pool containing:

  • x₁: quantity of Token X
  • y₁: quantity of Token Y

Price Dynamics Framework

Initial Price of Token Y:

P(Y_{init}) = \frac{x_1}{y_1}

When swapping x2​ of Token X for y2​ of Token Y, the received amount is:

y_2 = \frac{x_2 \times y_1}{x_1 + x_2}

Final Price Calculation:

P(Y_{final}) = \frac{x_1 + x_2}{y_1 - y_2} =

(x_1 + x_2) \div \left(y_1 - \frac{x_2 \times y_1}{x_1 + x_2}\right) =

(x_1 + x_2) \div \left(\frac{x_1 \times y_1 + x_2 \times y_1 - x_2 \times y_1}{x_1 + x_2}\right) =

(x_1 + x_2) \div \left(\frac{x_1 \times y_1}{x_1 + x_2}\right) =

(x_1 + x_2) \times \left(\frac{x_1 + x_2}{x_1 \times y_1}\right) =

P(Y_{final}) = \frac{(x_1 + x_2)^2}{x_1 \times y_1}

Price Slippage Derivation

The percentage price slippage is determined by:

\text{DEX Price Slippage} = \frac{P(Y_{final})}{P(Y_{init})} - 1 =

P(Y_{final}) \div P(Y_{init}) - 1 =

\frac{(x_1 + x_2)^2}{x_1 \times y_1} \div \frac{x_1}{y_1} - 1 =

\frac{(x_1 + x_2)^2}{x_1 \times y_1} \times \frac{y_1}{x_1} - 1 =

\frac{(x_1 + x_2)^2}{x_1^2} - 1 =

\frac{x_1^2 + 2x_1x_2 + x_2^2}{x_1^2} - \frac{x_1^2}{x_1^2} =

\text{DEX Price Slippage} = \frac{2x_1x_2 + x_2^2}{x_1^2}

Liquidity Ratio (LR) Concept

Introducing the Liquidity Ratio:

LR = \frac{x_2}{x_1}

We can express slippage purely in terms of LR:

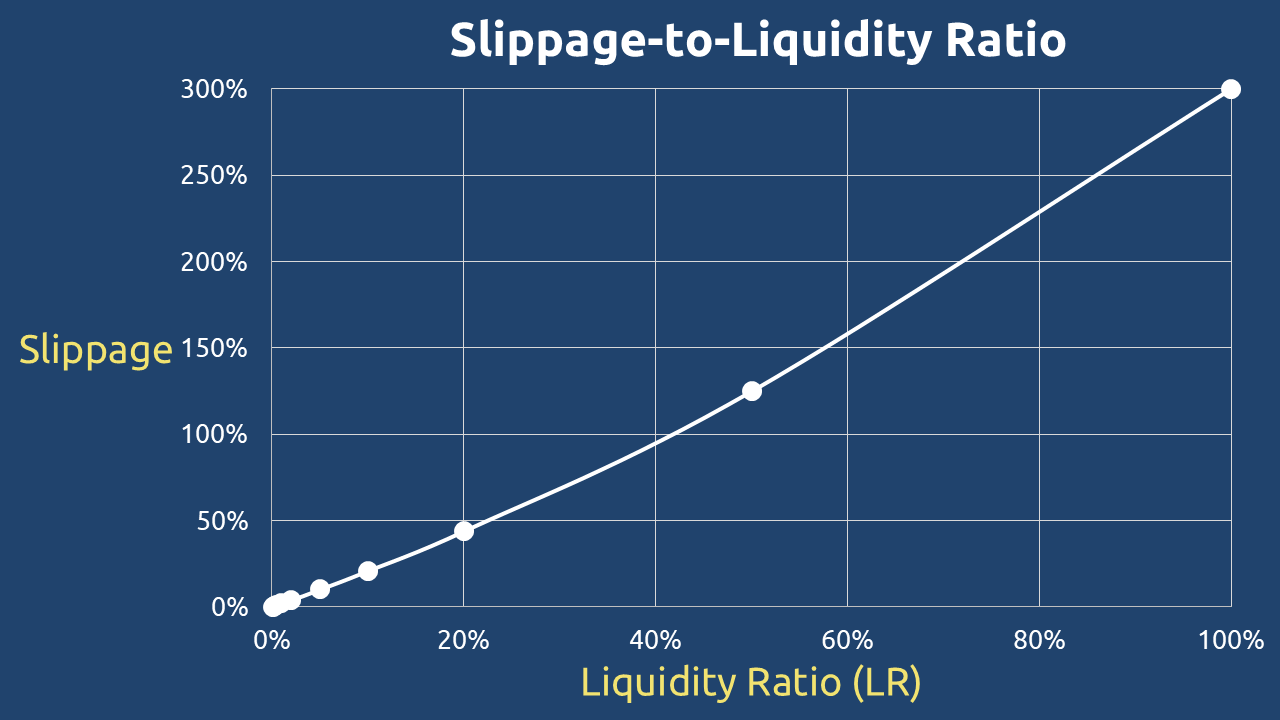
\text{DEX Price Slippage} = \left(\frac{x_2}{x_1}\right)^2 + 2 \times \frac{x_2}{x_1} = LR^2 + 2 \times LR

Figure 1. Slippage-to-Liquidity Ratio.

Key Insights:

  • Slippage depends solely on Token X liquidity parameters
  • Quadratic relationship between LR and slippage
  • Quadratic relationship between LR and slippage

Reverse Calculation: LR from Target Slippage

The quadratic equation can be solved to estimate the target LR based on the target DEX Price Slippage.

\text{DEX Price Slippage}_{target} = LR_{target}^2 + 2 \times LR_{target}

LR_{target}^2 + 2 \times LR_{target} - \text{DEX Price Slippage}_{target} = 0

LR_{target} = \frac{-2 + \sqrt{4 + 4 \times \text{DEX Price Slippage}_{target}}}{2}

LR_{target} = -1 + \sqrt{1 + \text{DEX Price Slippage}_{target}}

LR_{target} = \sqrt{1 + \text{DEX Price Slippage}_{target}} - 1

Practical Application

Example Pool:

  • QD(DAI)e1 = 100,000 DAI
  • QD(eGHST)e1 = 10,000 eGHST

For 5% slippage:

LR_{target} = \sqrt{1 + 0.05} - 1 \approx 0.02469 or 2.649%

Optimal Trade Size:

Q(DAI)_{e1} = 0.02469 \times 100000 = 2469.51 \text{ DAI}

This framework enables traders to precisely calculate expected price impacts and optimize their trade sizes in decentralized liquidity pools.

Tags: , , ,