Liquidity Provider Fundamentals: Price Impact from LP Contributions (Part 4)

You are currently viewing Liquidity Provider Fundamentals: Price Impact from LP Contributions (Part 4)

Understanding Price Impact in Liquidity Provision

In this final installment on LP contributions, we analyze how adding liquidity affects token prices—a crucial consideration for protocols like ghostDAO when designing LP-based monetary policies.

Price Impact Mechanics

Initial Setup:

x1: reserves of Token X

y1: reserves of Token Y

Original price of Token Y in terms of Token X:

\displaystyle P(Y)_1 = \frac{x_1}{y_1}

After swapping xs of Token X for ys of Token Y:

x1 + xs: reserves of Token X

y1 – ys: reserves of Token Y

New price:

\displaystyle P(Y)_2 = \frac{x_1 + x_s}{y_1 - y_s}

Price Impact Calculation

The relative price change is:

\displaystyle \frac{P(Y)_2}{P(Y)_1} = \frac{x_1 + x_s}{y_1 - y_s} \div \frac{x_1}{y_1} = \frac{x_1 + x_s}{y_1 - y_s} \times \frac{y_1}{x_1} = \frac{x_1 y_1 + x_s y_1}{x_1 (y_1 - y_s)}

Substituting ys (from swap mechanics):

\displaystyle y_s = \frac{x_s \times (1 - f) \times y_1}{x_1 + (1 - f) \times x_s}

\displaystyle \frac{P(Y)_2}{P(Y)_1} = \frac{x_1 y_1 + x_s y_1}{x_1 \times \left(y_1 - \frac{x_s \times (1 - f) \times y_1}{x_1 + (1 - f) \times x_s}\right)} =

\displaystyle \frac{x_1 y_1 + x_s y_1}{x_1 \times \left(\frac{y_1 \times (x_1 + (1-f) \times x_s)}{x_1 + (1-f) \times x_s} - \frac{x_s \times (1-f) \times y_1}{x_1 + (1-f) \times x_s}\right)} =

\displaystyle \frac{x_1 y_1 + x_s y_1}{x_1 \times \left(\frac{y_1 x_1 + x_s y_1 (1-f) - x_s y_1 (1-f)}{x_1 + (1-f) \times x_s}\right)} =

\displaystyle \frac{x_1 y_1 + x_s y_1}{x_1 \times \left(\frac{y_1 x_1}{x_1 + (1-f) \times x_s}\right)} = \frac{x_1 y_1 + x_s y_1}{\left(\frac{x_1^2 y_1}{x_1 + (1-f) \times x_s}\right)} =

\displaystyle \frac{x_1 y_1 + x_s y_1}{1} \div \frac{x_1^2 y_1}{x_1 + (1-f) \times x_s} = \frac{y_1 \times (x_1 + x_s)}{1} \times \frac{x_1 + (1-f) \times x_s}{x_1^2 y_1} =

\displaystyle \frac{(x_1 + x_s) \times (x_1 + (1 - f) \times x_s)}{x_1^2}

Exact Price Impact Derivation

We begin with the exact formulation of price impact after liquidity provision. Let’s systematically derive the relationship between added liquidity and the resulting price change.

Key Substitution

Let’s define:

\displaystyle \sqrt{Z} = \sqrt{(x_1 \times (2 - f))^2 + 4x_a x_1 \times (1 - f)}

Price Ratio Expansion

The price impact ratio develops as:

\displaystyle \frac{P(Y)_2}{P(Y)_1} = \frac{(x_1 + x_s) \times (x_1 + (1 - f) \times x_s)}{x_1^2} =

Substituting the Exact Swap Amount xs

Plugging in the precise swap quantity yields:

\displaystyle \frac{\left(x_1 + \frac{-x_1 \times (2 - f) + \sqrt{Z}}{2 \times (1 - f)}\right) \times \left(x_1 + (1 - f) \times \frac{-x_1 \times (2 - f) + \sqrt{Z}}{2 \times (1 - f)}\right)}{x_1^2} =

Through methodical expansion and cancellation

\displaystyle \frac{\left(\frac{x_1 \times (2 \times (1 - f))}{2 \times (1 - f)} + \frac{-x_1 \times (2 - f) + \sqrt{Z}}{2 \times (1 - f)}\right) \times \left(x_1 + (1 - f) \times \frac{-x_1 \times (2 - f) + \sqrt{Z}}{2 \times (1 - f)}\right)}{x_1^2} =

\displaystyle \frac{\left(\frac{2x_1 \times (1 - f) - x_1 \times (2 - f) + \sqrt{Z}}{2 \times (1 - f)}\right) \times \left(x_1 + \frac{-x_1 \times (2 - f) + \sqrt{Z}}{2}\right)}{x_1^2} =

\displaystyle \frac{\left(\frac{2x_1 - 2x_1 f - 2x_1 + x_1 f + \sqrt{Z}}{2 \times (1 - f)}\right) \times \left(\frac{2x_1 - x_1 \times (2 - f) + \sqrt{Z}}{2}\right)}{x_1^2} =

\displaystyle \frac{\left(\frac{-x_1 f + \sqrt{Z}}{2 \times (1 - f)}\right) \times \left(\frac{2x_1 - 2x_1 + x_1 f + \sqrt{Z}}{2}\right)}{x_1^2} = \frac{\left(\frac{-x_1 f + \sqrt{Z}}{2 \times (1 - f)}\right) \times \left(\frac{x_1 f + \sqrt{Z}}{2}\right)}{x_1^2} =

\displaystyle \frac{\left(\frac{Z - (x_1 f)^2}{4 \times (1 - f)}\right)}{x_1^2} = \frac{Z - (x_1 f)^2}{4 x_1^2 \times (1 - f)}

Final Simplification

Substituting back Z:

\displaystyle \frac{(x_1 \times (2 - f))^2 + 4x_a x_1 \times (1 - f) - (x_1 f)^2}{4x_1^2 \times (1 - f)} =

\displaystyle \frac{4x_1^2 - 4x_1^2 f + x_1^2 f^2 + 4x_1 x_a - 4x_1 x_a f - x_1^2 f^2}{4x_1^2 \times (1 - f)} =

\displaystyle \frac{4x_1^2 - 4x_1^2 f + 4x_1 x_a - 4x_1 x_a f}{4x_1^2 \times (1 - f)} = \frac{4x_1 \times (x_1 - x_1 f + x_a - x_a f)}{4x_1 \times x_1 \times (1 - f)} =

\displaystyle \frac{x_1 - x_1 f + x_a - x_a f}{x_1 \times (1 - f)} = \frac{x_1 \times (1 - f) + x_a \times (1 - f)}{x_1 \times (1 - f)} =

\displaystyle \frac{(x_1 + x_a) \times (1 - f)}{x_1 \times (1 - f)} = \frac{x_1 + x_a}{x_1}

Price Impact Formula

The percentage change simplifies elegantly to:

\displaystyle \frac{P(Y)_2}{P(Y)_1} - 1 = \frac{x_1 + x_a}{x_1} - 1 = \frac{x_1 + x_a - x_1}{x_1} = \frac{x_a}{x_1}

Where LR is the Liquidity Ratio

\displaystyle LR = \frac{x_a}{x_1}

Thus

\displaystyle \frac{P(Y)_2}{P(Y)_1} - 1 = LR

Key Insight:

Despite the complex intermediate steps, the final price impact depends linearly on the proportion of added liquidity (LR).

Simplified Price Impact Approximation

While the exact calculation provides precise results, we can derive a useful approximation that’s easier to work with in practice. This approximation becomes particularly valuable when making quick estimates or working with smaller liquidity additions.

Core Approximation

We begin with the simplified swap amount:

\displaystyle x_{s,approx} = x_a \times \frac{1}{2 - f}

Price Impact Derivation

The approximate price ratio develops as:

\displaystyle \frac{P(Y)_{2,approx}}{P(Y)_1} = \frac{(x_1 + x_{s,approx}) \times (x_1 + (1 - f) \times x_{s,approx})}{x_1^2} =

Substituting our approximation:

\displaystyle \frac{\left(x_1 + x_a \times \frac{1}{2 - f}\right) \times \left(x_1 + (1 - f) \times x_a \times \frac{1}{2 - f}\right)}{x_1^2} =

Through systematic expansion:

\displaystyle \frac{\left(\frac{x_1 \times (2 - f)}{2 - f} + \frac{x_a \times 1}{2 - f}\right) \times \left(\frac{x_1 \times (2 - f)}{2 - f} + \frac{(1 - f) \times x_a \times 1}{2 - f}\right)}{x_1^2} =

\displaystyle \frac{\left(\frac{x_1 \times (2 - f) + x_a}{2 - f}\right) \times \left(\frac{x_1 \times (2 - f) + x_a \times (1 - f)}{2 - f}\right)}{x_1^2} =

\displaystyle \frac{x_1^2 \times (2 - f)^2 + x_1 x_a \times (2 - f) \times (1 - f) + x_1 x_a \times (2 - f) + x_a^2 \times (1 - f)}{x_1^2 \times (2 - f)^2} =

\displaystyle \frac{x_1^2 \times (2 - f)^2 + x_1 x_a \times (2 - f) \times (2 - f) + x_a^2 \times (1 - f)}{x_1^2 \times (2 - f)^2} =

\displaystyle \frac{x_1^2 \times (2 - f)^2 + x_1 x_a \times (2 - f)^2 + x_a^2 \times (1 - f)}{x_1^2 \times (2 - f)^2} =

\displaystyle 1 + \frac{x_a}{x_1} + \left(\frac{x_a}{x_1}\right)^2 \times \frac{1 - f}{(2 - f)^2}

Percentage Price Change

The relative price impact becomes:

\displaystyle \frac{P(Y)_{2,approx}}{P(Y)_1} - 1 \approx 1 + \frac{x_a}{x_1} + \left(\frac{x_a}{x_1}\right)^2 \times \frac{1 - f}{(2 - f)^2} - 1 = \left(\frac{x_a}{x_1}\right)^2 \times \frac{1 - f}{(2 - f)^2} + \frac{x_a}{x_1}

Expressed in terms of Liquidity Ratio (LR):

\displaystyle \frac{P(Y)_{2,approx}}{P(Y)_1} - 1 \approx LR^2 \times \frac{1 - f}{(2 - f)^2} + LR

Practical Implications

  1. Dominant Linear Term: For small LR (<20%), the linear term dominates, making the approximation accurate
  2. Quadratic Correction: The squared term becomes noticeable for larger liquidity additions
  3. Fee Sensitivity: The impact of trading fees (f) is contained within the quadratic term’s coefficient
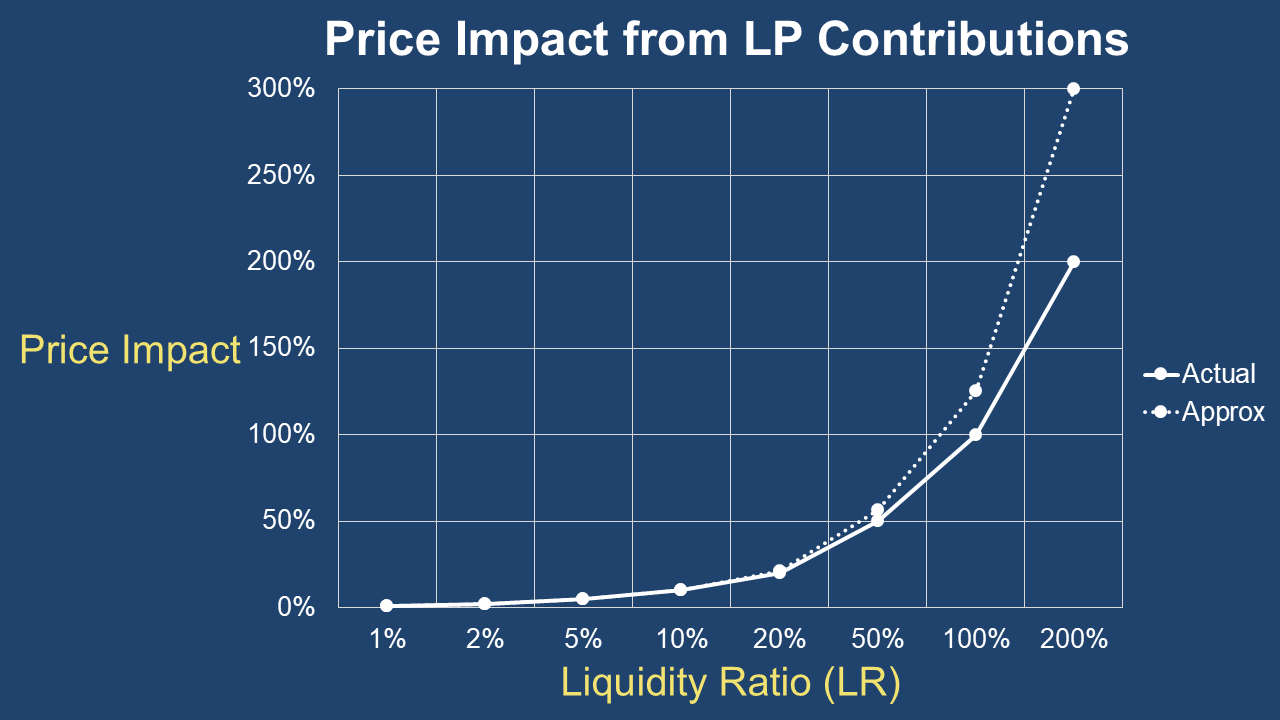
Figure 1. Price Impact-to-Liquidity Ratio.

Accuracy Comparison

  • At LR = 10%: Approximation error < 0.5%
  • At LR = 20%: Approximation error ≈ 2%
  • At LR = 50%: Consider using exact formula instead

This approximation provides a valuable shortcut for estimating price impacts during liquidity provision, especially useful for:

  • Quick mental calculations
  • Protocol design iterations
  • Small to moderate liquidity additions

The exact and approximate methods converge for practical purposes when LR ≤ 20%, validating the use of this simpler approach.

What is GHOST Chain?

GHOST Chain is a decentralized EVM bridge with a privacy layer providing a much needed cross-chain interoperability and anonimity in the web3 space.

Become Validator | GHOST Chain | ghostDAO Litepaper
Tags: , , ,