Liquidity Provider Fundamentals: “k” Without DEX Fees (Part 5)

You are currently viewing Liquidity Provider Fundamentals: “k” Without DEX Fees (Part 5)

Recap: What is k?

At last, we’ve arrived at the core concept – the product constant k. But is it really as straightforward as it seems?

From our earlier discussions, we know that k is simply the product of reserves in a decentralized exchange liquidity pool:

\displaystyle k_1 = x_1 \times y_1

Here, x1 and y1 represent the reserves of Token X and Token Y, respectively.

Theoretical Scenario: A DEX with No Fees

To build a solid intuition around k, let’s first examine a simplified, fee-free DEX environment. This theoretical approach helps clarify how k behaves under different conditions.

k Remains Constant During Swaps

When a trader swaps x₂ of Token X for y₂ of Token Y, the product k stays unchanged.

\displaystyle k_1 = (x_1 + x_2) \times (y_1 - y_2)

Using this relationship, we can derive the amount of Token Y (y₂) the trader receives:

\displaystyle y_2 = \frac{x_2 \times y_1}{x_1 + x_2}

This ensures that k remains balanced before and after the swap.

Figure 1. k Dynamics.

k Changes When Adding or Removing Liquidity

Unlike swaps, liquidity provision and withdrawal directly impact k.

Adding Liquidity Expands k

If a liquidity provider deposits x₂ and y₂ tokens in the correct ratio, the new k becomes:

\displaystyle {k_{after\,adding\,liquidity}} = (x_1 + x_2) \times (y_1 + y_2)

Since both reserves increase, k grows proportionally. The magnitude of this expansion depends on the size of the new deposits relative to the existing reserves.

Figure 2. k After Adding Liquidity.

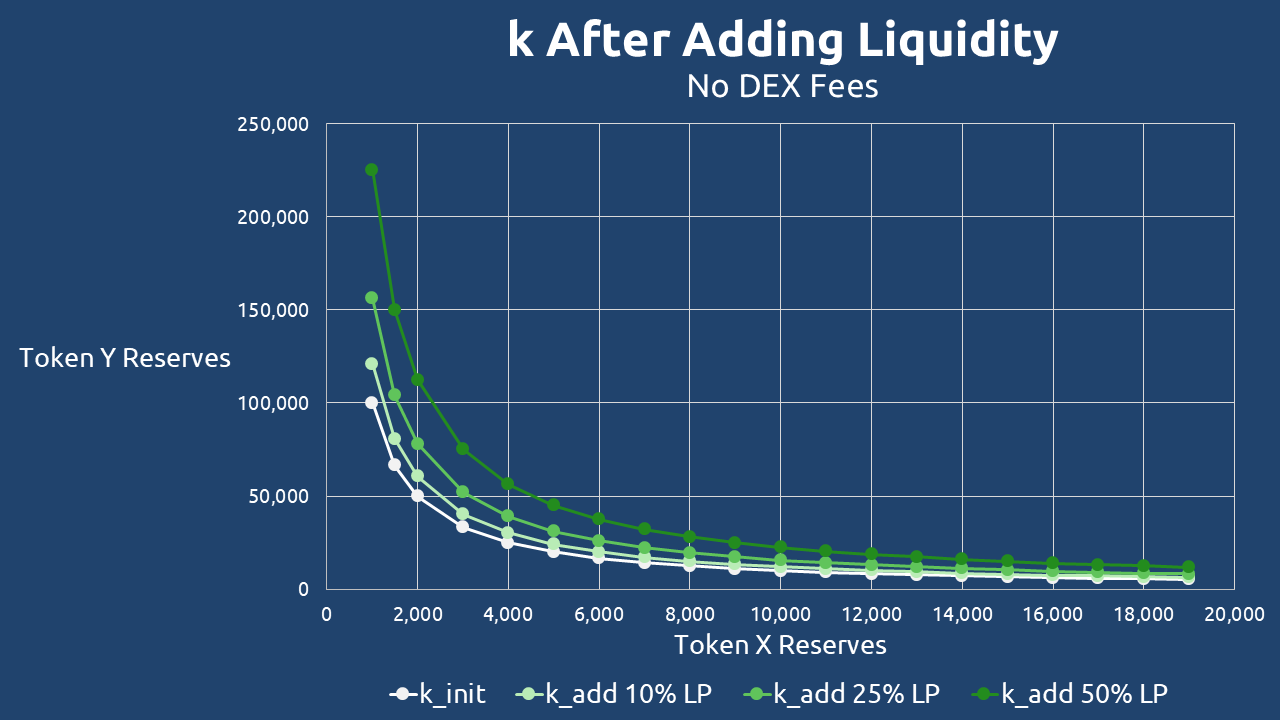
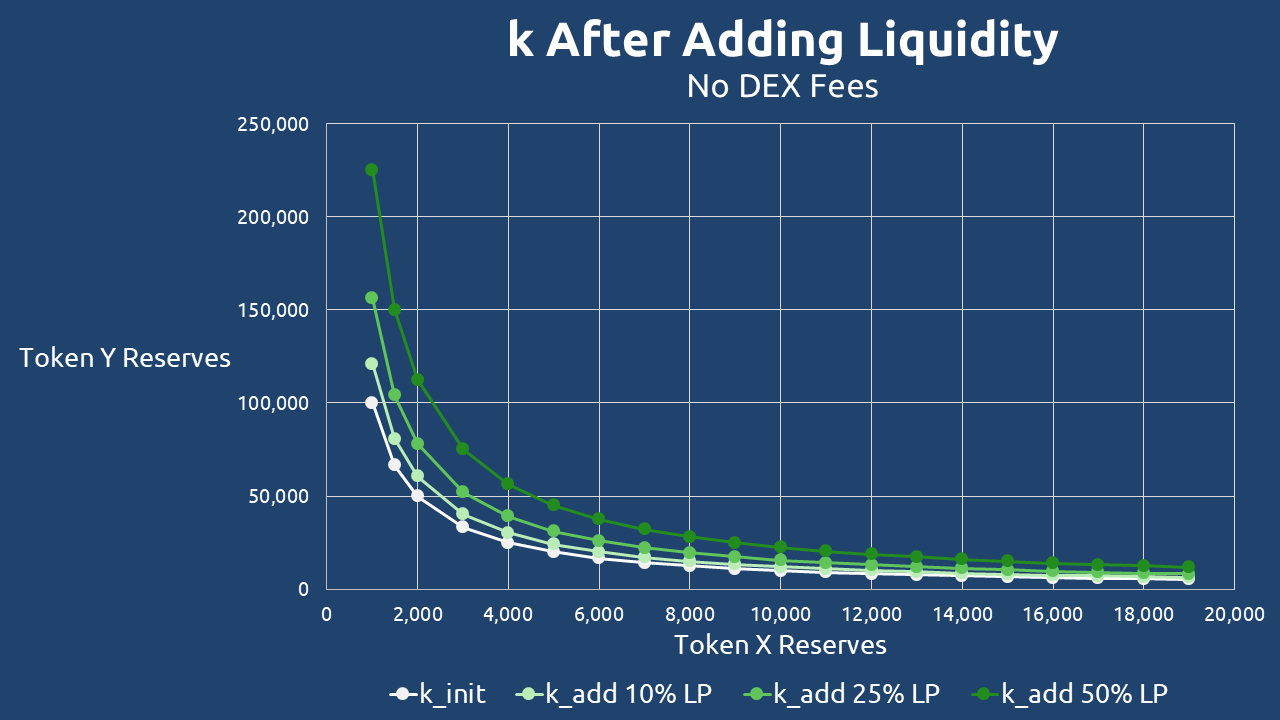
To illustrate how liquidity provision affects the product constant k, let’s consider a DEX pair with initial reserves of 10,000 Token X and 10,000 Token Y. In this scenario, liquidity providers deposit additional tokens at 10%, 25%, and 50% of the existing reserves.

Initial State (Before Adding Liquidity)

The starting value of k is calculated as:

\displaystyle k_{init} = 10,\!000 \times 10,\!000 = 100 \times 10^6

After Adding 10% Liquidity

New reserves: 11,000 Token X and 11,000 Token Y

\displaystyle {k_{add\,10\%\,LP}} = (10,\!000 + 1,\!000) \times (10,\!000 + 1,\!000) = 121 \times 10^6

After Adding 25% Liquidity

New reserves: 12,500 Token X and 12,500 Token Y

\displaystyle {k_{add\,25\%\,LP}} = (10,\!000 + 2,\!500) \times (10,\!000 + 2,\!500) = 156.25 \times 10^6

After Adding 50% Liquidity

New reserves: 15,000 Token X and 15,000 Token Y

\displaystyle {k_{add\,50\%\,LP}} = (10,\!000 + 5,\!000) \times (10,\!000 + 5,\!000) = 225 \times 10^6

Notice how k increases quadratically with proportional liquidity additions. A 10% increase in reserves leads to a 21% rise in k, while a 50% increase more than doubles k (from 100mm to 225mm).

This demonstrates how liquidity expansion directly amplifies the pool’s depth and trading capacity. In the next section, we’ll examine how k behaves when liquidity is withdrawn.

Removing Liquidity Contracts k

Conversely, when a liquidity provider withdraws x₂ and y₂ tokens (in the correct ratio), k decreases:

\displaystyle {k_{after\, removing\, liquidity}} = (x_1 - x_2) \times (y_1 - y_2)

With both reserves reduced, k shrinks accordingly.

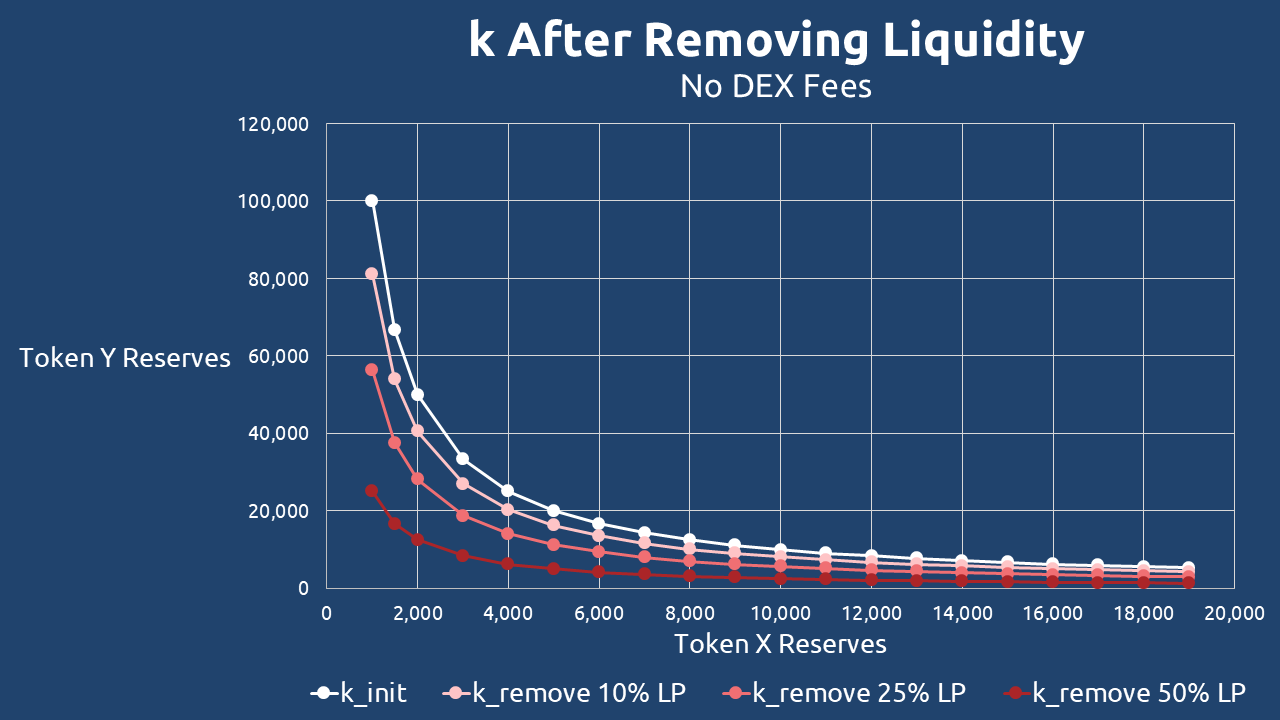
Figure 3. k After Removing Liquidity.

Let’s examine a practical example of how removing liquidity affects the product constant k. We’ll analyze a DEX pool containing 10,000 Token X and 10,000 Token Y, where liquidity providers withdraw 10%, 25%, and 50% of the current reserves.

Initial State (Before Removing Liquidity)

The starting value of k is calculated as:

\displaystyle k_{init} = 10,\!000 \times 10,\!000 = 100 \times 10^6

After Removing 10% Liquidity

New reserves: 9,000 Token X and 9,000 Token Y

\displaystyle {k_{remove\,10\%\,LP}} = (10,\!000 - 1,\!000) \times (10,\!000 - 1,\!000) = 81 \times 10^6

After Removing 25% Liquidity

New reserves: 7,500 Token X and 7,500 Token Y

\displaystyle {k_{remove\,25\%\,LP}} = (10,\!000 - 2,\!500) \times (10,\!000 - 2,\!500) = 56.25 \times 10^6

After Removing 50% Liquidity

New reserves: 5,000 Token X and 5,000 Token Y

\displaystyle {k_{remove\,50\%\,LP}} = (10,\!000 - 5,\!000) \times (10,\!000 - 5,\!000) = 25 \times 10^6

k decreases quadratically when liquidity is withdrawn proportionally. A 10% reserve reduction lowers k by 19% (from 100mm to 81mm), while a 50% reserve reduction causes k to drop by 75% (from 100mm to 25mm).

Key Takeaways

  • Swaps: keep k constant (assuming no DEX fees).
  • Deposits: increase k by expanding reserves.
  • Withdrawals: decrease k by reducing reserves.

What is GHOST Chain?

GHOST Chain is a decentralized EVM bridge with a privacy layer providing a much needed cross-chain interoperability and anonimity in the web3 space.

Become Validator | GHOST Chain | ghostDAO Litepaper
Tags: , , , ,