Liquidity Provider Fundamentals: How DEX Fees Offset Impermanent Loss (Part 8)

You are currently viewing Liquidity Provider Fundamentals: How DEX Fees Offset Impermanent Loss (Part 8)

We now arrive at a crucial concept: how DEX trading fees compensate for Impermanent Loss (IL). While most sources vaguely mention this relationship, few explain the exact mechanics.

Let’s revisit our previous IL formula:

\displaystyle IL (\%) = \frac{2}{d + 1} \times \frac{y_2}{y_1} - 1

Now, we’ll adjust for price changes (d) and DEX fees.

Price Ratio (d) with DEX Fees

Define d as the price change ratio:
\displaystyle d = \frac{x_1 y_2}{x_2 y_1}

From this, we derive:
\displaystyle x_1 y_2 = d \times x_2 y_1

Multiply both sides by \displaystyle y_1 y_2:
\displaystyle x_1 y_2 \times y_1 y_2 = d \times x_2 y_1 \times y_1 y_2

\displaystyle x_1 y_1 y_2^2 = d \times x_2 y_2 y_1^2

Since DEX fees increase k (without liquidity additions/withdrawals, only swaps), we use:

\displaystyle k_1 = x_1 y_1 \quad \text{and} \quad k_2 = x_2 y_2

Substituting k1 and k2:
\displaystyle k_1 \times y_2^2 = d \times k_2 \times y_1^2

Solving for \displaystyle \frac{y_2}{y_1}:
\displaystyle \frac{y_2^2}{y_1^2} = d \times \frac{k_2}{k_1}

\displaystyle \frac{y_2}{y_1} = \sqrt{d \times \frac{k_2}{k_1}}

Plugging back into the IL equation:
\displaystyle IL (\%) = \frac{2}{d + 1} \times \sqrt{d \times \frac{k_2}{k_1}} - 1 = \sqrt{\frac{k_2}{k_1}} \times \frac{2\sqrt{d}}{d + 1} - 1

Key Implications:

  • If no swaps occur, \displaystyle k_1 = k_2
  • If swaps occur, \displaystyle k_1 > k_2  (fees accumulate)
  • The term \displaystyle \sqrt{\frac{k_2}{k_1}} > 0 (DEX Liquidity Ratio, DLR) reduces IL impact

Numerical Examples: IL vs. DEX Fees

Define DLR (DEX Liquidity Ratio):
\displaystyle DLR = \sqrt{\frac{k_2}{k_1}}

Figure 1. Impermanent Loss vs. DEX Fees.

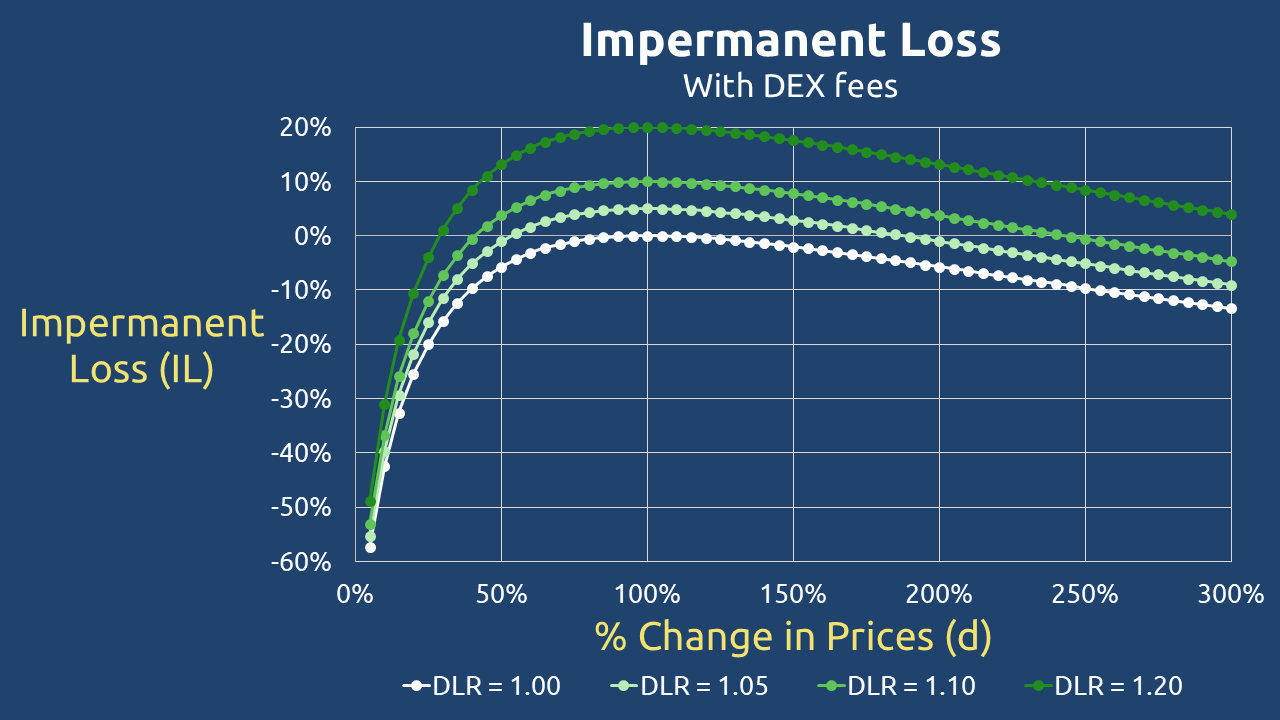
When DLR = 1.05

  • d = 25% (Token X drops by 75%) → IL = -16.0%
  • d = 50% (Token X drops by 50%) → IL = -1.0%
  • d = 75% (Token X drops by 25%) → IL = 3.9%
  • d = 125% (Token X rises by 25%) → IL = 4.3%
  • d = 150% (Token X rises by 50%) → IL = 2.9%
  • d = 200% (Token X rises by 100%) → IL = -1.0%
  • d = 300% (Token X rises by 200%) → IL = -9.1%

✅ Profit Zone: d = 53% to 188%

When DLR = 1.10

  • d = 25% (Token X drops by 75%) → IL = -12.0%
  • d = 50% (Token X drops by 50%) → IL = 3.7%
  • d = 75% (Token X drops by 25%) → IL = 8.9%
  • d = 125% (Token X rises by 25%) → IL = 9.3%
  • d = 150% (Token X rises by 50%) → IL = 7.8%
  • d = 200% (Token X rises by 100%) → IL = 3.7%
  • d = 300% (Token X rises by 200%) → IL = -4.7%

✅ Profit Zone: d = 41% to 243%

When DLR = 1.20

  • d = 25% (Token X drops by 75%) → IL = -4.0%
  • d = 50% (Token X drops by 50%) → IL = 13.1%
  • d = 75% (Token X drops by 25%) → IL = 18.8%
  • d = 125% (Token X rises by 25%) → IL = 19.3%
  • d = 150% (Token X rises by 50%) → IL = 17.6%
  • d = 200% (Token X rises by 100%) → IL = 13.1%
  • d = 300% (Token X rises by 200%) → IL = 3.9%

✅ Profit Zone: d = 29% to 347%

Key Takeaways

  • DEX fees reduce IL impact – Higher DLR (more fees) expands the profitable price range.
  • Fee accumulation matters – Even with large price swings, sufficient fees can turn IL into gains.
  • Practical insight – liquidity providers should monitor DLR to assess whether fees outweigh IL.
Tags: , , ,