Liquidity Provider Fundamentals: Impermanent Loss Without DEX Fees (Part 7)

Understanding Impermanent Loss (IL)

Impermanent Loss (IL) is one of the most critical – yet often misunderstood – concepts for liquidity providers in decentralized exchanges (DEXes).

What Causes Impermanent Loss?

When you provide liquidity to a DEX, you take the opposite side of every trade.

If traders swap Token X → Token Y, liquidity providers effectively swap Token Y → Token X.
This changes the pool’s reserves, altering the relative pricesof the tokens.

IL occurs when the value of your LP position becomes lower than simply holding the tokens (HODLing) due to price fluctuations.

Key Assumptions for Simplifying IL Calculation

To isolate IL’s mechanics, we assume:

No DEX fees (ignoring fee income for now).
No liquidity additions/removals (only swaps occur).
LP’s stake is relatively small (doesn’t impact reserves significantly).

Mathematical Derivation of Impermanent Loss

1. Initial Setup

Starting Pool reserves:

x of Token X
y of Token Y

Starting prices (denominated in Token Y):

$\displaystyle P(X) = \frac{y}{x}$
$\displaystyle P(Y) = 1$

Alice, liquidity provider, deposits:

x₁ of Token X
y₁ of Token Y

Her deposit maintains the initial price ratio:

$\displaystyle P(X)_1 = \frac{y_1}{x_1} = \frac{y}{x} = P(X)$
$\displaystyle P(Y)_1 = 1 = P(Y)$

Value of Alice’s LP position (in Token Y):

$\displaystyle \text{Value(LP)}_1 = x_1 \times P(X)_1 + y_1 \times P(Y)_1 = x_1 \times \frac{y_1}{x_1} + y_1 \times 1 = 2y_1$

2. After Swaps (New Reserves & Prices)

Alice’s new reserves:

x₂ of Token X
y₂ of Token Y

New prices:

$\displaystyle P(X)_2 = \frac{y_2}{x_2}$
$\displaystyle P(Y)_2 = 1$

Value of Alice’s LP position (in Token Y):

$\displaystyle \text{Value(LP)}_2 = x_2 \times P(X)_2 + y_2 \times P(Y)_2 = x_2 \times \frac{y_2}{x_2} + y_2 \times 1 = 2y_2$

Since we are solving for IL, which is spread across all LP providers equally (within a specific timeframe), Alice could have just HODLed her original set of reserves. Thus, the value of original reserves at x₁ and y₁ would now be priced at P(X)₂ and P(Y)₂, respectively. Alice’s HODLed value will be equal to:

$\displaystyle \text{Value(LP)}_{\text{HODL}} = x_1 \times P(X)_2 + y_1 \times P(Y)_2 = x_1 \times \frac{y_2}{x_2} + y_1$

Critical Assumption: Small LP Share

This calculation assumes Alice’s liquidity provision is insignificant compared to total reserves. If her stake were relatively large:

Withdrawing it would substantially impact pool reserves
The price P(X)₂ would be different (likely worse due to slippage)
The actual IL would be lower than calculated

3. Calculating Impermanent Loss (%)

Basic Formula

The percentage IL compares the LP value to the HODL value:

$\displaystyle \text{IL (\%)} = \frac{\text{Value(LP)}_2}{\text{Value(LP)}_{\text{HODL}}} - 1$

Simplifying the Expression

$\displaystyle IL\% = \frac{2y_2}{x_1 \frac{y_2}{x_2} + y_1} - 1 = \frac{2y_2}{x_1 \frac{y_2}{x_2} + y_1 \frac{x_2}{x_2}} - 1 = \frac{2y_2}{\frac{x_1 y_2 + x_2 y_1}{x_2}} - 1 =$

$\displaystyle \frac{2y_2}{1} \times \frac{x_2}{x_1 y_2 + x_2 y_1} - 1 = \frac{2x_2 y_2}{x_1 y_2 + x_2 y_1} - 1$

Introducing Price Ratio (d)

Define d as the price change ratio:

$\displaystyle d = \frac{P(X)_2}{P(X)_1} = P(X)_2 \div P(X)_1 = \frac{y_2}{x_2} \div \frac{y_1}{x_1} = \frac{y_2}{x_2} \times \frac{x_1}{y_1} = \frac{x_1 y_2}{x_2 y_1}$

This implies:

$\displaystyle x_1 y_2 = d \times x_2 y_1$

Substituting into the IL formula:

$\displaystyle IL\% = \frac{2x_2 y_2}{d x_2 y_1 + x_2 y_1} - 1 = \frac{2x_2 y_2}{x_2 y_1 (d + 1)} - 1 = \frac{2y_2}{y_1 (d + 1)} - 1 = \frac{2}{d + 1} \times \frac{y_2}{y_1} - 1$

Relating $\displaystyle \frac{y_2}{y_1}$ to d:

$\displaystyle x_1 y_2 = d \times x_2 y_1$

Multiplying both parts by $\displaystyle y_1 y_2$ :

$\displaystyle x_1 y_2 \times y_1 y_2 = d \times x_2 y_1 \times y_1 y_2$

$\displaystyle x_1 y_1 y_2^2 = d \times x_2 y_2 y_1^2$

k stays the same due to no DEX fees:

$\displaystyle k_1 = x_1 y_1$

$\displaystyle k_2 = x_2 y_2$

Replacing with k’s:

$\displaystyle k_1 y_2^2 = d \times k_2 y_1^2$

Final simplification to cancel out k’s:

$\displaystyle y_2^2 = d \times y_1^2 \implies d = \frac{y_2^2}{y_1^2} \implies \frac{y_2}{y_1} = \sqrt{d}$

Final IL formula:

$\displaystyle IL\% = \frac{2}{d + 1} \times \frac{y_2}{y_1} - 1 = \frac{2}{d + 1} \times \sqrt{d} - 1 = \frac{2\sqrt{d}}{d + 1} - 1$

Interpreting Impermanent Loss

The derived formula reveals several key insights about liquidity provision:

Price Sensitivity: IL occurs whenever d ≠ 1 (i.e., when prices change from their initial ratio)
IL is Inevitable: Large price moves in either direction cause losses
Convexity: The IL curve is convex, with losses accelerating for larger price movements
Compensation Mechanism: DEX fees offset IL, which we’ll analyze next

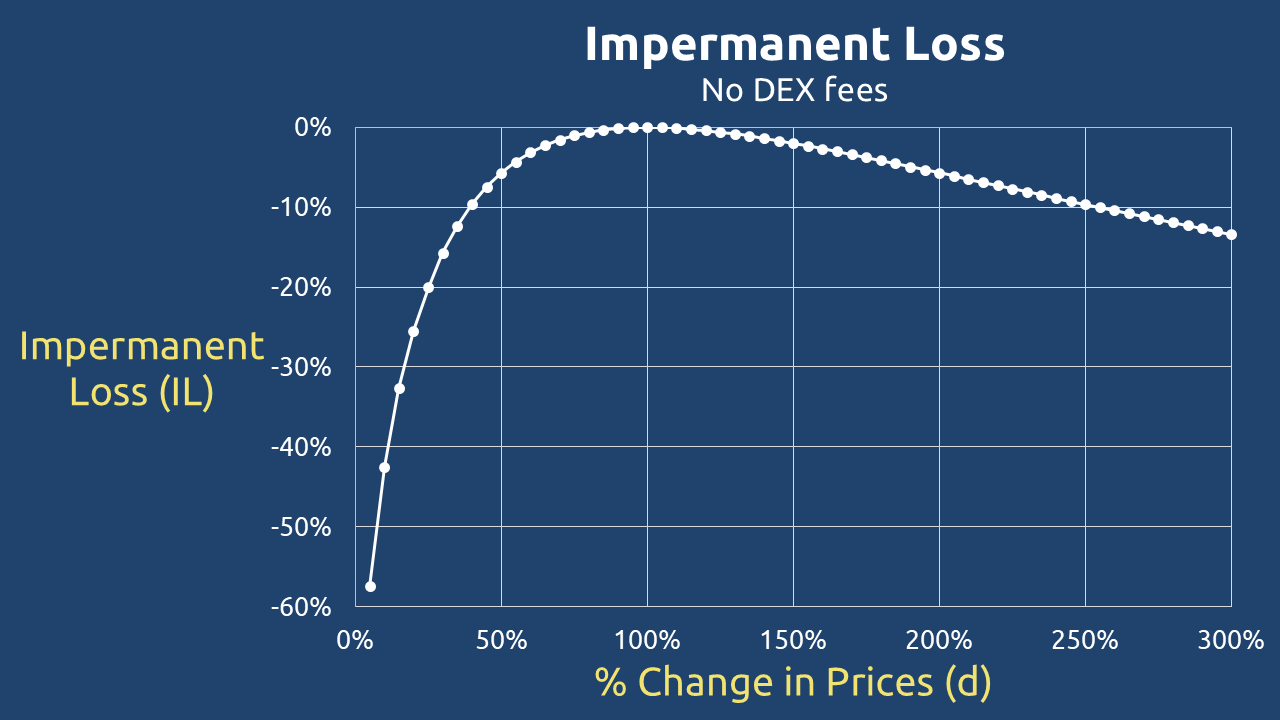
Figure 1. Impermanent Loss without DEX Fees.

IL Numerical Examples

d = 25% (Token X drops by 75%) → IL = -20.0%
d = 50% (Token X drops by 50%) → IL = -5.7%
d = 75% (Token X drops by 25%) → IL = -1.0%
d = 125% (Token X rises by 25%) → IL = -0.6%
d = 150% (Token X rises by 50%) → IL = -2.0%
d = 200% (Token X rises by 100%) → IL = -5.7%
d = 300% (Token X rises by 200%) → IL = -13.4%

This complete derivation shows why liquidity providers must earn sufficient fees to make market-making profitable despite inherent IL. The next segment will incorporate fee income into this framework.

What is GHOST Chain?

GHOST Chain is a decentralized EVM bridge with a privacy layer providing a much needed cross-chain interoperability and anonimity in the web3 space.

Become Validator | GHOST Chain | ghostDAO Litepaper